I expect Villain’s flop raise to be his only barrel if he is bluffing. That is, he’s usually going to check down his air and bet only if the river improves his hand to one that beats mine.
PokerStars No-Limit Hold’em, $4.00 BB (4 handed) – Poker-Stars Converter Tool from FlopTurnRiver.com
Hero (SB) ($709.80)
BB ($4005.10)
UTG ($413)
Button ($798.50)
Preflop: Hero is SB with K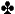
, 7
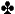
2 folds, Hero bets $16, BB calls $12
Flop: ($32) 9
, 7
, 2
(2 players)
Hero bets $24, BB raises to $72, Hero calls $48
Turn: ($176) 5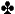 (2 players)
Hero checks, BB checks
River: ($176) Q (2 players)
Hero checks, BB bets $124, Hero raises to $621.80 (All-In), 1 fold
Total pot: $424 | Rake: $2
Results:
Hero didn’t show K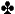, 7 (nothing).
Outcome: Hero won $422
Does he have the best hand when the Q falls? Often enough that I can’t call with a pure bluff catcher, I think. But can he call a shove, even with AQ? We’ll see…
How many strong hands do you play this way?
Sets and a turned straight, at least. His flop raise is pretty much always either a bluff or a hand good enough to bet the turn. Thus, there’s little reason not to slowplay a flopped monster.
When he checks behind the turn, he’s rarely calling a river bet. If I have a big hand, the best I can do is check and hope he either bluffs or rivered a hand good enough to value bet.
K7 is actually one of the weaker hands in my range by the time we get to the river, so turning it into a bluff is pretty reasonable even against a Villain capable of some big calls, which I didn’t think this guy was.
You probably already know this, but as it’s a somewhat obscure and (to me) interesting point of poker math, I’ll mention it anyway for those readers who might be interested:
When deciding whether shoving or calling is better in this situation, what percentage of his betting range is bluffs is irrelevant. It could even be zero.
This assumes that he will never call with a losing hand if you shove.
Let
b = the fraction of his range that consists of bluffs or other losing hands
c = the fraction of his range consisting of winners he will bet-call if you raise
f = the fraction of his range that is winners he will bet-fold if you raise
P = the pot after he bets
C = your cost of calling his bet
R = your cost of raising (including cost of calling)
The EV of just calling is therefore
EV(call) = Pb – Cf – Cc
The EV of shoving is
EV(raise) = Pb + Pf – Rc
Since the Pb term is the same in both, we can throw it out when comparing:
EV(raise) > EV(call) ?
Pf – Rc > -Cf – Cc ?
As this shows, the value of b is irrelevant in the decision whether to raise or call. It matters only if you’re trying to decide whether to raise, call or fold.
The above comparison can be further simplified, which makes calculations at the table a bit simpler. That’s because R = C + X, where X is the amount of the raise above the cost of calling:
Pf – Rc > -Cf – Cc
Pf – Cc – Xc > -Cf – Cc
Pf – Xc > – Cf
Pf + Cf > Xc
f/c > X/(P+C)
In your case
P = 300
C = 124
X = 497
so the question is whether the ratio of bet-folds to bet-calls is greater than the ratio of your additional cost of raising (X, not R) divided by the pot size plus your cost of calling:
f/c > 497/424
I find it easier to work with percentages so
f/(c+f) > 497/(424 + 497)
497/921 = 54%, so if he will fold more than 54% of his winners, raising is better than calling. (Note that 921 is the current pot size, 300, plus the total cost of raising, 621, and 497 is the cost of the raise excluding the cost of calling).
This comes up often enough that it’s worth being able to estimate it at the table. I would have rounded 497 up to 500 and 921 down to 900, which would have given me an answer of about 5/9 or 55%. Close enough for poker.
Lin –
That’s true, but it does affect the merit of check/shoving relative to check/folding. Since Andrew already decided check/calling wasn’t an option, I assume by that he means check/folding is better than check/calling. So in determining the best play, we’ll want to compare check/shoving to check/folding, not check/calling.
Okay, let me add a preamble:
In similar situations where, unlike this one, you’ve decided that calling is an option…
🙂